1.Sequential Search :

In sequential search elements are examined sequentially starting from the first clement. The process of searching terminates when the list is exhausted or a comparison results in success.

Algorithm for searching an element 'key' in an array 'a[ ]' having n elements : The search algorithm starts comparison between the first element of a[ ] and "key". As long as a comparison does not result in success, the algorithm proceeds to compare the next element of "a[ ]" with "key". The process terminates when the list is exhausted or the element is found.

#'C' function for sequential search.

                                    int sequential_search(int a[], int key, int n) 
                                    {
                                        int i = 0;
                                        while (i < n) 
                                        {
                                            if (a[i] == key)
                                            {
                                                return (i);
                                            }
                                            i++;
                                        }
                                        return (-1);
                                    }
                                

The function returns the index of th element in 'a[ ]' for successful search. A value "-1" is returned if the element is not found.

Array to be searched for

1. Start from the first element, compare "k" with each element "x".

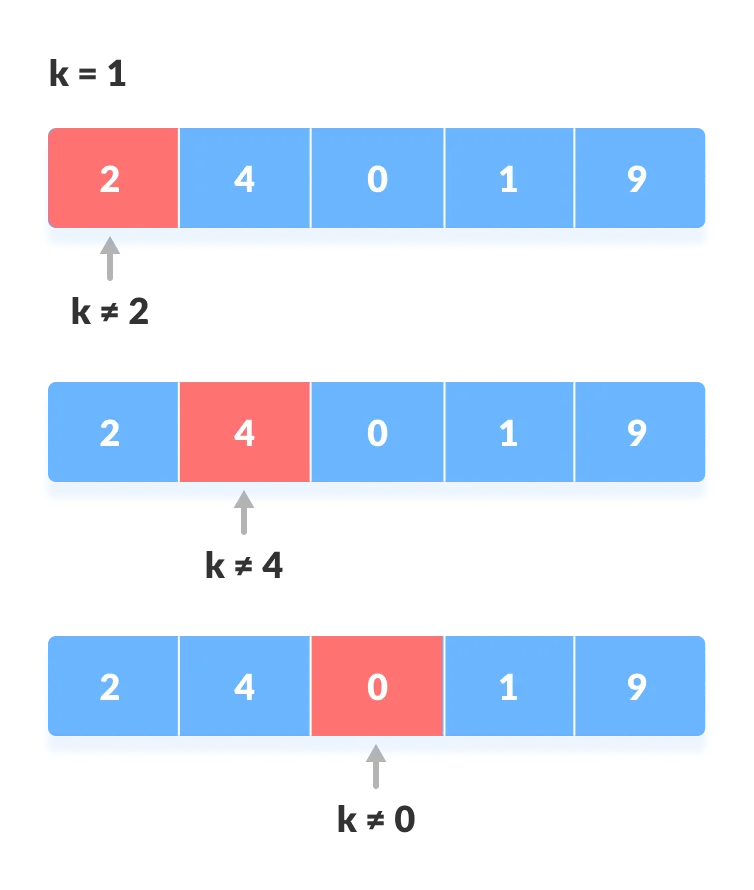
2. If "x == k", return the index.

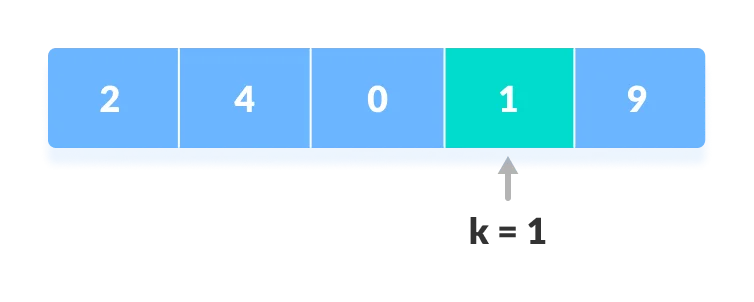
3. Else, return "elements not found"

#Complete program for linear search

                                // Linear Search in C++
    
                                #include 
                                using namespace std;
                                
                                int search(int array[], int n, int x) {
                                
                                  // Going through array sequencially
                                  for (int i = 0; i < n; i++){
                                         if (array[i] == x){
                                               return i;
                                         }
                                         return -1;
                                  }
                                };
                                
                                int main() {
                                  int array[] = {2, 4, 0, 1, 9};
                                  int x = 1;
                                  int n = sizeof(array) / sizeof(array[0]);
                                
                                  int result = search(array, n, x);
                                
                                  if(result == -1){
                                      cout << "Element not found" ;
                                  }
                                  else{
                                      cout << "Element found at index: "<< result;
                                  }
                                  
                                }
                            

2.Binary Search :

Linear search has a time complexity O(n). Such algorithms are not suitable for searching when number of elements is large.

Binary search exhibits much better timing behaviour in case of large volume of data with timing complexity : O(log2 n)

Number of comparisons for n = 2²⁰ (1 million)
Sequential search (in worst case) = 2²⁰
Binary search (in worst case) = log ₂2 ²⁰= 20 comparisons.

Linear search (sequential search) may need 1 million comparisons for searching an element in an array having 1 million elements. Binary search will require, just 20 comparisons for the same task. Binary search uses a much better method of searching. Binary search is applicable only when the given array is sorted.

1.This method makes a comparison between the "key" (element to be searched) and the middle element of the array.
2.Since elements are sorted, comparisons may result in either a match or comparison could be continued with either left half of elements or right half of the elements.
3.Left half of elements could be selected by simply making j = c-1
4.Right half of element could be selected by simply making i = c+1
5.Process of selecting either the left half or the right half continues until the element is found or element is not there.

# 'C' Function for binary search (Non-recursive)

                                                    
                    int bin_search(int a[], int i, int j, int key){
                        int c;
                        c = (i + j) / 2;
                        while (a[c] != key && i <= j){
                        /* search as long as element is not found and it could be there*/
                            if (key > a[c]){
                                i = c + 1; // select right half
                            }
                            else{
                                j = c - 1; //select left half
                            }
                            c = (i + j) / 2;
                        }
                        if (i <= j){
                            return (c);
                        }
                        return (-1);
                    }
                                                
                                            

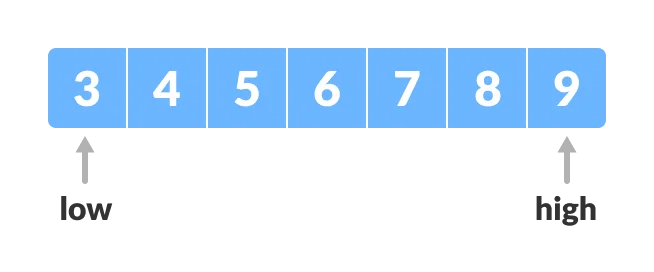
1.Let "x = 4" be the element to be searched :

2.Set two pointers low and high at the lowest and the highest positions respectively.

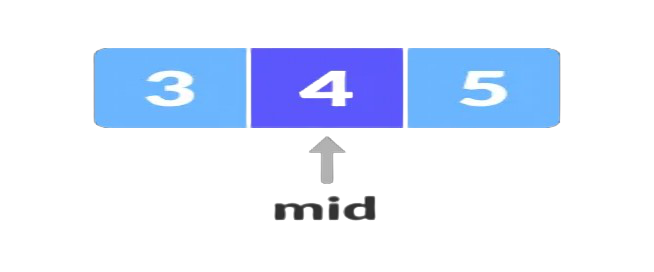
3.Finding the middle element "mid" of the array i.e., " arr[(low + high)/2] = 6 ".

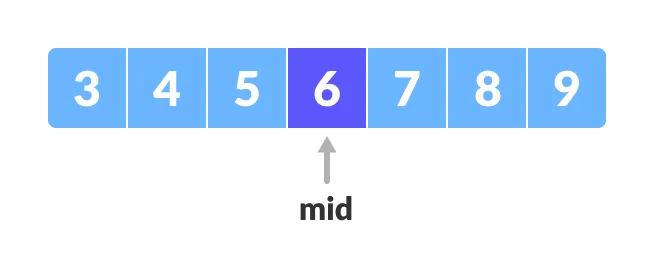
4.If " x == mid ", then return " mid ",compare the element to be searchedwith " m ".

5.If " x > mid ", compare " x " with the middle element of the elements on hte right side of " mid ". This is done by setting " low " to " low = mid + 1".

6.Else, compare " x " with the middle element of the elements on the left side of " mid ". This is done by setting " high " to " high = mid - 1".

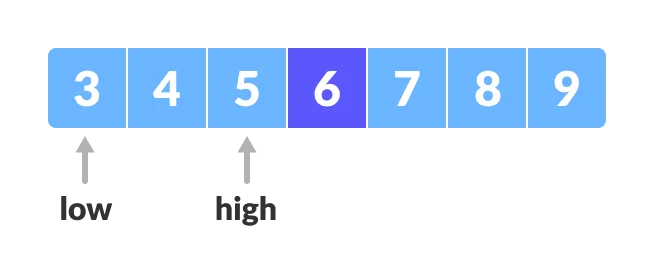
7.Repeat steps 3 to 6 until low meets high.

8." x = 4 " is found.

# Complete program for Binary Search

                    // Binary Search in C++
                    #include 
                    using namespace std;
                                                        
                    int binarySearch(int array[], int x, int low, int high) {
                                                            
                    // Repeat until the pointers low and high meet each other
                    while (low <= high) {
                            int mid = low + (high - low) / 2;                                
                            if (array[mid] == x)
                            return mid;
                                                        
                            if (array[mid] < x)
                            low = mid + 1;
                    
                            else
                            high = mid - 1;
                        }
                        return -1;
                    }
                    
                    int main(void) {
                            int array[] = {3, 4, 5, 6, 7, 8, 9};
                            int x = 4;
                            int n = sizeof(array) / sizeof(array[0]);
                            int result = binarySearch(array, x, 0, n - 1);
                            if (result == -1)
                                cout<<"Not found :" ;
                            else
                                cout<<"Element is found at index %d", result);
                    }